由一道课本例题引发的探究教学
- 分类:互动沙龙
- 发布:殷妃
- 日期:2021-05-25 10:32
- 阅读量:1140
由一道课本例题引发的探究教学
长沙市二十一中 姚贵丰
人教A版七年级下册第八章课本P99例题:
据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物,怎样划分这块土地,使甲、乙这两种作物的总产量的比是3:4?
分析:如图8.3—1,一种种植方案为:甲、乙两种作物的种植区域分别为长方形AEFD和BCFE.此时设AE=xm,BE=ym,根据问题中涉及长度、产量的数量关系,

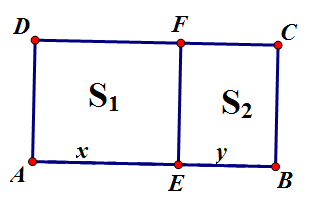
(图8.3—1)
过长方形土地的长边上离一端 处,作这条边的垂线,把这块土地分为两块长方形土地,较大的一块土地种 种作物,较小的一块土地种 种作物。
大多数老师按照课本上思路分析解题,学生课堂学到的仅是关于二元一次方程组的应用解题方法,就题解题,收获较小。仔细推敲,发现本题有较大的探索空间。可以启发学生思考:解答思维是怎样形成的?解题思维能否发散些?笔者想进行一番探究。
探究
由课本上分析,“求截得的长方形长、宽是多少”,若改为“截的的两个图形的面积是多少”。设这两个几何图形面积分别为S1、S2,根据题意,S1+S2=20000,S1:S2=3:4,计算可得,S1=12000,S2=8000.这样,将局限在二元一次方程组的应用问题。为此,笔者在课堂教学中大胆探索,将“求土地长、宽是多少”转化为“几何图形的分割”,学生思维更广阔了。可将问题转变为“已知长200m、宽100m的长方形,现要将它分为面积分别为12000m2和8000m2的两个规则的几何图形,怎么分?”
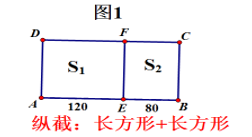
1. 纵截:“长方形+长方形”
如图1所示,宽不变仍为100m,根据长方形面积公式,只要把长200m分为120m、80m就可以啦。这种解法的思路是固定宽,改变长,将长分为两个部分。一般学生容易想到,也是课本的思想。
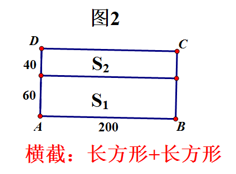
2. 横截:“长方形+长方形”
如图2所示,长不变仍为200m,根据长方形面积公式,只要把宽100m分为60m,40m就可以啦。这种解法的思路是固定长,改变宽,将宽分为两个部分。通过追问,学生可以想到,也是课本设计者希望学生能做到的。
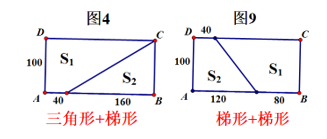
3. 斜截:“三角形+梯形”,或“梯形+梯形”
如图4所示,宽不变仍为100m,根据三角形面积公式,只要把长200m划出160m,高即原长方形的宽100m就可以啦。这种解法的思路是固定宽作为三角形高,改变长,高已为100m,满足三角形底边长160m。通过联想学生可以想到,也是第1、2种分割方法的延伸。有了这种分割方法的基础,“梯形+梯形”如图9所示的分割方法就不难了,可以说只要老师一点拨,学生就想到了。
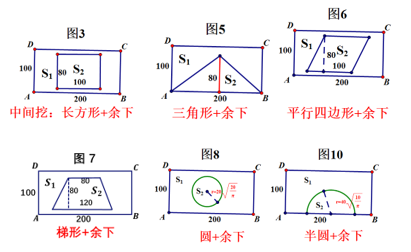
4. 中间挖:“长方形+余下部分”、“三角形+余下部分”、“平行四边形+余下部分”“梯形+余下部分”、“圆+余下部分”、“半圆+余下部分”
如图3所示,在原来的大长方形内找一个符合条件的小长方形,即面积为8000m2的长方形,只要长≤200m,宽≤100m就可以啦,如图3中的长为100m,宽为80m的长方形,也可以长为160m,宽为50m等等。通过启发思考,学生可以做到。有了这个分析的基础,学生思维的大门被打开,下面这些分割一蹴而就。三角形+余下部分”如图5所示、“平行四边形+余下部分”如图6所示、“梯形+余下部分”如图7所示、“圆+余下部分”如图8所示、“半圆+余下部分”如图10所示